Appearance Optimization of Environmental Conditioning Equipment: Multi-Physical Field Coupling & Optimization Algorithm Solution

Abstract

For indoor air quality control equipment optimization, data on ACs, humidifiers, and purifiers is collected. Shape optimization models are built for each to analyze shape factor impacts on functions and obtain optimal shapes and sizes[1]. Then a 3-in-1 device appearance optimization model is established to maximize energy efficiency, human comfort, purification, and humidification effects.

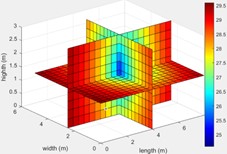
First, air conditioning temperature field optimization analyzes unit placement, inlet/outlet, and wind speed/volume. With heat conduction, Navier-Stokes, and energy equations, a model of indoor airflow and temperature is built. Particle swarm optimizer, finite difference discretizes, SIMPLE solves, and adaptive mesh improves accuracy for uniform temperature.

Secondly, for air purifier shape optimization, a model linking purification effect and shape is set up, with a multi-physical coupling model of particle motion, airflow, pollutant diffusion, and filtration efficiency for efficient purification. The finite difference method discretizes relevant equations and turns partial differential equations into algebraic ones for solving, and the gradient descent method[2] is employed to obtain optimal shape parameters, ultimately finding the best shape and size to maximize purification.

Thirdly, for humidifier performance optimization, consider its role in vapor processes. Build a math model integrating evaporation rate, diffusion, and shape geometry for multi-quantity coupling. Use simulated annealing[3] to iteratively find the optimal, achieving precise humidification control and optimal shape/size.

Finally, integrate models of the previous three problems for the three-in-one environmental regulator. Build a hierarchical optimization model with multi-physical field coupling[4]. Use multi-objective particle swarm genetic algorithm for overall performance optimization[5]. Explore field-volume coupling-based hierarchical nested optimization algorithm to handle multifunctional integration.

This study constructs a full optimization design system. Despite physical model simplification limitations, it's improvable. The results are extendable to other environmental conditioning equipment optimization.