Uniform Decay for the Viscoelastic Kirchhoff-Type Equations with Memory and Delay Terms
Abstract
In this paper, we investigate the initial boundary value problem of the viscoelastic Kirchhoff-type equations with memory and delay terms. We investigate the initial boundary value problem of viscoelastic Kirchhoff-type equations with memory and delay terms. The analysis assumes relatively weak conditions for the relaxation function g. This paper introduces a new framework for analyzing decay properties under weaker conditions, improving upon previous results in the literature. Finally, we prove that the system energy exhibits exponential and polynomial decay rates, which depend on the behavior of the relaxation function ɡ. This provides new insights into the energy decay properties of Kirchhoff-type viscoelastic wave equations under weaker conditions on the relaxation function, and provides a valuable technical framework for exploring the decay properties of more complex partial differential equations.
References
[2] Liu W., Li G., & Hong L. (2014). General decay and blow-up of solutions for a system of viscoelastic equations of Kirchhoff type with strong damping. Journal of Function Spaces, 2014(1), 284809. https://doi.org/10.1155/2014/284809
[3] Daewook K. (2016). Stabilization for the viscoelastic kirchhoff type equation with a nonlinear source. East Asian Mathematical Journal, 32(1), 117-128. https://doi.org/10.7858/eamj.2016.012
[4] Daewook K. (2016). Asymptiotic behavior for the viscoelastic kirchhoff type equation with an internal time-varying delay term. East Asian Mathematical Journal, 32(3), 399-412. https://doi.org/10.7858/eamj.2016.030
[5] Yang Z. (2020). Blow-up and lifespan of solutions for a nonlinear viscoelastic Kirchhoff equation. Results in Mathematics, 75(3), 84. https://doi.org/10.1007/s00025-020-01223-2
[6] Yang X., Zhang J., & Wang S. (2020). Stability and dynamics of a weak viscoelastic system with memory and nonlinear time-varying delay. Discrete & Continuous Dynamical Systems: Series A, 40(3). https://doi.org/10.3934/dcds.2020084
[7] Liao M., Guo B., & Zhu X. (2020). Bounds for blow-up time to a viscoelastic hyperbolic equation of Kirchhoff type with variable sources. Acta Applicandae Mathematicae, 170(1), 755-772. https://doi.org/10.1007/s10440-020-00357-3
[8] Mezouar N., & Boulaaras S. (2020). Global existence and decay of solutions for a class of viscoelastic Kirchhoff equation. Bulletin of the Malaysian Mathematical Sciences Society, 43, 725-755. https://doi.org/10.1007/s40840-018-00708-2
[9] Li C., & Jin K. P. (2020). General decay results for viscoelastic systems with memory and time-varying delay. Mathematical Methods in the Applied Sciences, 45(8), 4397-4407. https://doi.org/10.1002/mma.8045
[10] Zuo J., Rahmoune A., & Li Y. (2022). General Decay of a Nonlinear Viscoelastic Wave Equation with Balakrishnˆan-Taylor Damping and a Delay Involving Variable Exponents. Journal of Function Spaces, 2022(1), 9801331. https://doi.org/10.1155/2022/9801331
[11] Mezouar N., Boulaaras S., & Allahem A. (2020). Global existence of solutions for the viscoelastic Kirchhoff equation with logarithmic source terms. Complexity, 2020(1), 7105387. https://doi.org/10.1155/2020/7105387
[12] Pi,skin E., Boulaaras S., & Irkil N. (2025). Local existence and blow up for a nonlinear viscoelastic kirchhoff-type equation with logarithmic nonlinearity. Kragujevac Journal of Mathematics, 49(3), 335-351. https://doi.org/10.46793/KgJMat2503.335P
[13] Berrimi S., & Messaoudi S. (2006). Existence and decay of solutions of a viscoelastic equation with a nonlinear source. Nonlinear Analysis: Theory, Methods & Applications, 64(10), 2314-2331. https://doi.org/10.1016/j.na.2005.08.015
[14] Lasiecka I., & Tataru D. (1993). Uniform boundary stabilization of semilinear wave equations with nonlinear boundary damping. Differential Integral Equations, 6(3), 507-533. https://doi.org/10.57262/die/1370378427
[15] Cavalcanti M., & Oquendo H. (2003). Frictional versus viscoelastic damping in a semilinear wave equation. SIAM Journal on Control and Optimization, 42(4), 1310-1324. https://doi.org/10.1137/S0363012902408010
[16] Jin K. P., Liang J., & Xiao T. J. (2014). Coupled second order evolution equations with fading memory: Optimal energy decay rate. Journal of Differential Equations, 257(5), 1501-1528. https://doi.org/10.1016/j.jde.2014.05.018
[17] Jin K. P. (2022). Indirect stabilization of coupled abstract evolution equations with memory: Different propagation speeds. Mathematical Methods in the Applied Sciences, 45(8), 4451-4467. https://doi.org/10.1002/mma.8048
[18] Li C., & Jin K. P. (2022). General decay results for viscoelastic systems with memory and time-varying delay. Mathematical Methods in the Applied Sciences, 45(8), 4397-4407. https://doi.org/10.1002/mma.8045
[19] Nicaise S., Valein J., & Fridman E. (2009). Stability of the heat and of the wave equations with boundary time-varying delays. Discrete and Continuous Dynamical Systems-Series S, 2(3), 559-581. https://doi.org/10.3934/dcdss.2009.2.559
[20] Alabau-Boussouira F., Cannarsa P., & Sforza D. (2008). Decay estimates for second order evolution equations with memory. Journal of Functional Analysis, 254(5), 1342-1372. https://doi.org/10.1016/j.jfa.2007.09.012
[21] Alabau-Boussouira F. (2005). Convexity and weighted integral inequalities for energy decay rates of nonlinear dissipative hyperbolic systems. Applied Mathematics and Optimization, 51(1), 61-105. https://doi.org/10.1007/s00245
[22] Alabau-Boussouira F., Nicaise S., & Pignotti C. (2014). Exponential stability of the wave equation with memory and time delay. New Prospects in Direct, Inverse and Control Problems for Evolution Equations, 1-22. https://doi.org/10.1007/978-3-319-11406-41
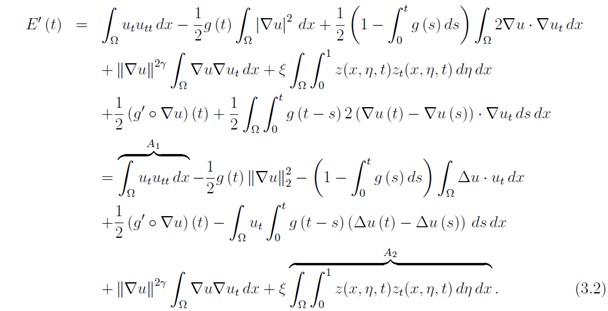

This work is licensed under a Creative Commons Attribution 4.0 International License.
Copyright for this article is retained by the author(s), with first publication rights granted to the journal.
This is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).








1.png)














