Multidimensional and Nonlinear Fractional Langevin Equations: Advancing the Theory in of Anomalous Diffusion

Abstract

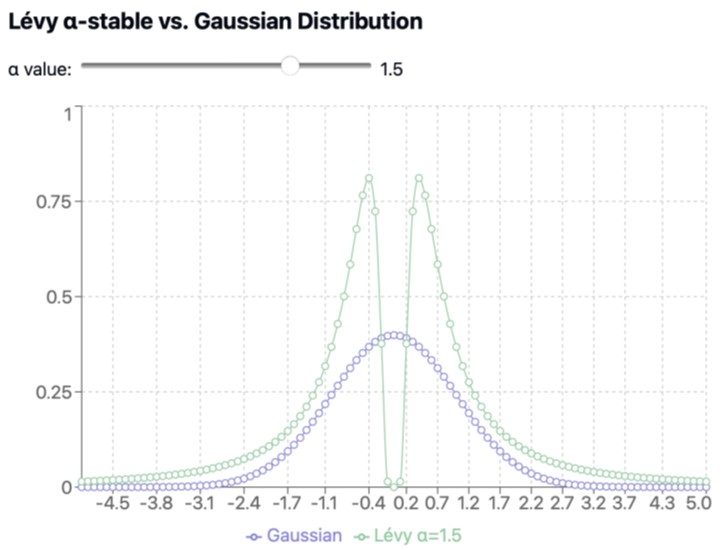
This paper presents a comprehensive theoretical analysis of fractional Langevin equations (FLEs) and their applications in modeling anomalous diffusion processes. We extend the classical FLE framework in several significant directions to address the complexities observed in various physical, biological, and social systems. First, we derive a multidimensional extension of the FLE, providing a robust tool for studying anomalous diffusion in higher-dimensional spaces. Second, we incorporate non-Gaussian Lévy α-stable noise into the FLE, enabling the description of systems characterized by heavy-tailed distributions and extreme events. Third, we develop a nonlinear variant of the FLE to model more intricate restoring forces and potential landscapes. Finally, we analyze a generalized FLE with different orders of fractional derivatives for the inertial and friction terms, offering a flexible framework capable of capturing a wider range of anomalous diffusion phenomena.

For each extension, we prove the existence and uniqueness of solutions, derive the corresponding probability distributions, and analyze the scaling behavior of the mean squared displacement in the long-time limit. Our results demonstrate how these generalized FLEs can describe various regimes of anomalous diffusion, from subdiffusive to superdiffusive behavior. This work provides a unified theoretical foundation for understanding and modeling complex diffusive processes across diverse disciplines, paving the way for more accurate descriptions of systems exhibiting memory effects, non-Gaussian statistics, and multiscale dynamics.