On Stability Estimate of Optimal Transport Maps Using m-th Polynomial Convexity

Kei Leong Chen

doi:10.30560/ijas.v7n1p1

Kei Leong Chen Shenzhen College of International Education, China

DOI: https://doi.org/10.30560/ijas.v7n1p1

Keywords: Optimal transport, Covexity, Optimiazation

Abstract

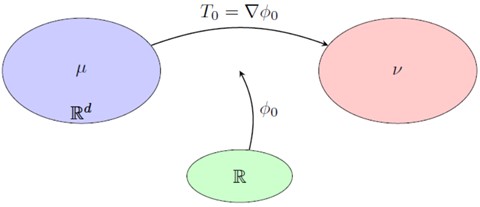
In 1781, Gaspard Monge first proposed the practical problem of relocating building materials while minimizing workers’ effort. Mathematically, the problem can be reiterated as finding a mapping T0 that transforms a random variable (X) following probability measure (μ) into a random variable (Y) following probability measure (ν), with minimal cost. Afterward, it has been widely studied and applied in statistics, machine learning, and economics, which concern the study of “distance” between usually a pair of probability distributions. The focus of this paper is centered on investigating and generalizing stability estimates for optimal transport plans, particularly through the lens of strong polynomial convexity. Building on previous research using plug-in estimators to strengthen the convergence rate of discrete or semi-discrete estimators for optimal transport plans, this paper introduces a novel stability estimate leveraging L-Lipschitz continuity and a paradigmatic methodology based on polynomial convexity, the understanding of which remains limited.

References

[1] Deb, N., Ghosal, P., & Sen, B. (2021). Rates of estimation of optimal transport maps using plug-in estimators via barycentric projections. Advances in Neural Information Processing Systems, 34, 29736-29753.
[2] McCann, R. J. (1995). Existence and uniqueness of monotone measure-preserving maps. https://doi.org/10.1215/S0012-7094-95-08013-2
[3] Li, W., & Nochetto, R. H. (2021). Quantitative stability and error estimates for optimal transport plans. IMA Journal of Numerical Analysis, 41(3), 194-1965. https://doi.org/10.1093/imanum/draa045
[4] Delalande, A., & Merigot, Q. (2023). Quantitative stability of optimal transport maps under variations of the target measure. Duke Mathematical Journal, 172(17), 3321-3357. https://doi.org/10.1215/00127094-2022-0106
[5] Ambrosio, L., Caffarelli, L. A., Brenier, Y., Buttazzo, G., Villani, C., Salsa, S., Ambrosio, L., & Pratelli, A. (2003). Existence and stability results in the L1 theory of optimal transportation. Optimal Transportation and Applications: Lectures given at the CIME Summer School, held in Martina Franca, Italy, September 2-8, 2001, 123-160. https://doi.org/10.1007/978-3-540-44857-0_5
[6] Vacher, A., & Vialard, F. X. (2023). “Semi-dual unbalanced quadratic optimal transport: fast statistical rates and convergent algorithm. In International Conference on Machine Learning. PMLR, 34734-34758.
[7] Gangbo, W., & McCann, R. J. (2000). Shape recognition via wasserstein distance. Quarterly of Applied Mathematics, 705-737. https://doi.org/10.1090/qam/1788425
[8] Galichon, A. (2021). The unreasonable effectiveness of optimal transport in economics. arXiv preprint arXiv:2107.04700.
[9] Boyd, S. P., & Vandenberghe, L. (2004). Convex optimization. Cambridge university press, 2004. https://doi.org/10.1017/CBO9780511804441
[10] Villani, C. (2003). Topics in optimal transportation, volume 58 of graduate. Studies in Mathematics. https://doi.org/10.1090/gsm/058
[11] Peyr´e, G., & Cuturi, M. et al. (2019). Computational optimal transport: With applications to data science. Foundations and Trends® in Machine Learning, 11(5-6), 355-607. https://doi.org/10.1561/2200000073
[12] Mena, G., & Niles-Weed, J. (2019). Statistical bounds for entropic optimal transport: Sample complexity and the central limit theorem. Advances in Neural Information Processing Systems, 32.