The LQR Based On Optimized Tuning PD Controller For AVR System
Abstract
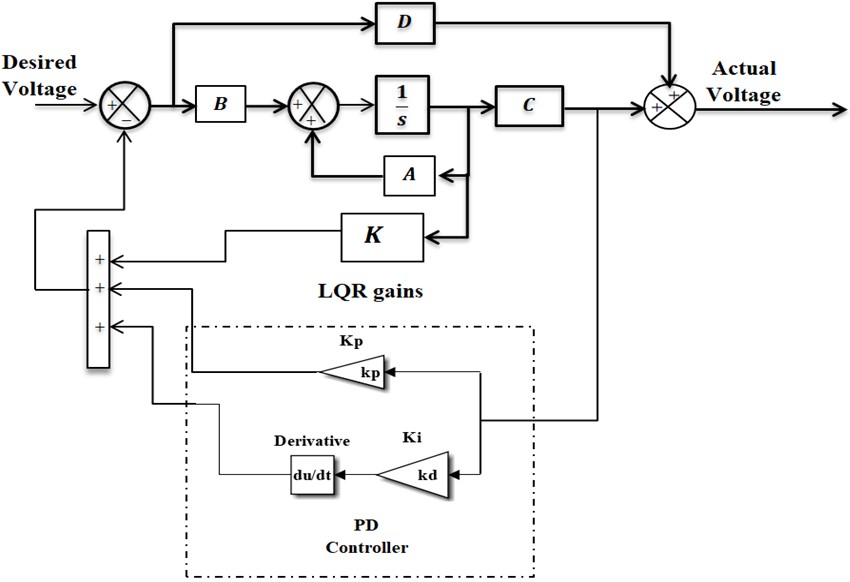
This study presents a Linear Quadratic Regulator (LQR) based on an optimizing PD controller to improve the dynamic performance of an automatic voltage regulation (AVR) system. Biogeography-based optimization (BBO) is used to adjust the controller gains, and the Mean Absolute Percentage Error (MAPE) cost function is used to ensure effective performance. To demonstrate the advantages of the suggested controller, a transient study was conducted and compared to a standard PD, LQR, and then used PD-LQR in terms of (Rising time, Settling time, Max Overshoot, and Peak time). Finally, simulations demonstrated that the PD-LQR gives satisfactory outcomes and a quicker reaction, which was evidently represented in the recommended controller's strong and steady performance in enhancing the transient analysis of the AVR system.
References
[2] Abood, L. H., & Bashra, K. O. (2021). Design of fractional order PID controller for AVR system using whale optimization algorithm. Indonesian Journal of Electrical Engineering and Computer Science 23.3, (2021), 1410-1418.
[3] Chatterjee, S., & Mukherjee, V. (2016). PID controller for automatic voltage regulator using teaching–learning based optimization technique. International Journal of Electrical Power & Energy Systems 77 (2016), 418-429.
[4] H. Shayeghi, A. Y., & Hashemi, Y. (2015). Optimal design of a robust discrete parallel FP+ FI+ FD controller for the automatic voltage regulator system. International Journal of Electrical Power & Energy Systems, (67), 66-75. https://doi.org/10.1016/j.ijepes.2014.11.013
[5] Karam, E. H., & Noor, M. M. (2017). Improve Linear Quadratic Regulator by Particle Swarm Optimization Algorithms for Two Wheeled Self Balancing Mobile robot." Iraqi Journal for Electrical And Electronic Engineering, 13(2).
[6] B. Ozgenc, M. S. A., & Altas, I. H. (2020). A Hybrid Optimization Approach to Design Optimally Tuned PID Controller for an AVR System. International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), 2020, pp. 1-5. https://doi.org/10.1109/HORA49412.2020.9152898.
[7] Karam, E. H., Noor, S. Abdul-Jaleel, & Basma, J. S. (2020). Design of hybrid Neuro-Robust deadbeat controller for higher order linear systems based on optimized mixed reduction method. International Review of Applied Sciences and Engineering, 11(3), 251-260.
[8] Maghfiroh, H., Ataka, A., Wahyunggoro, O., & Cahyadi, A. I. (2013, November). Optimal energy control of dc motor speed control: Comparative study. In 2013 International Conference on Computer, Control, Informatics and Its Applications (IC3INA) (pp. 89-93).
[9] Brian, R. C. (2008). The Design of PID Controllers using Ziegler Nichols Tuning” March 2008.
[10] Simon, D. (2008). Biogeography-based optimization. IEEE Transactions on Evolutionary Computation, 12(6), 702-713.
[11] Mohammed, S., & Mohamed, F. K. (2012). Application of Biogeography based optimization in tuning a PID controller for nonlinear systems. IEEE, 2012.
[12] Haiping, Ma, Dan, Simon, Patrick, S., Yang, Z. L., & Fei, M. R. (2017). Biogeography-Based Optimization: A 10-Year Review. IEEE Transactions on Emerging Topics in Computational Intelligence, 1(5), OCTOBER 2017.
[13] Jadoo, E. H., & Ekhlas, H. K. (2020). FPGA IMPLEMENTATION OF SECOND ORDER SLIDING MODE BASED ON ST ALGORITHM FOR TYPE I DIABETES. Journal of Engineering and Sustainable Development (JEASD) 24. Special_ Issue_2020.

This work is licensed under a Creative Commons Attribution 4.0 International License.
Copyright for this article is retained by the author(s), with first publication rights granted to the journal.
This is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).








1.png)














